https://blog.csdn.net/zhihua_oba/article/details/73776553

EM算法（Expectation Maximization Algorithm）详解

主要内容
- EM算法简介
- 预备知识
  - 极大似然估计
  - Jensen不等式
- EM算法详解
  - 问题描述
  - EM算法推导
  - EM算法流程

1、EM算法简介

EM算法是一种迭代优化策略，由于它的计算方法中每一次迭代都分两步，其中一个为期望步（E步），另一个为极大步（M步），所以算法被称为EM算法（Expectation Maximization Algorithm）。EM算法受到缺失思想影响，最初是为了解决数据缺失情况下的参数估计问题，其算法基础和收敛有效性等问题在Dempster，Laird和Rubin三人于1977年所做的文章Maximum likelihood from incomplete data via the EM algorithm中给出了详细的阐述。其基本思想是：首先根据己经给出的观测数据，估计出模型参数的值；然后再依据上一步估计出的参数值估计缺失数据的值，再根据估计出的缺失数据加上之前己经观测到的数据重新再对参数值进行估计，然后反复迭代，直至最后收敛，迭代结束。

EM算法作为一种数据添加算法，在近几十年得到迅速的发展，主要源于当前科学研究以及各方面实际应用中数据量越来越大的情况下，经常存在数据缺失或者不可用的的问题，这时候直接处理数据比较困难，而数据添加办法有很多种，常用的有神经网络拟合、添补法、卡尔曼滤波法等等，但是EM算法之所以能迅速普及主要源于它算法简单，稳定上升的步骤能非常可靠地找到“最优的收敛值”。随着理论的发展，EM算法己经不单单用在处理缺失数据的问题，运用这种思想，它所能处理的问题更加广泛。有时候缺失数据并非是真的缺少了，而是为了简化问题而采取的策略，这时EM算法被称为数据添加技术，所添加的数据通常被称为“潜在数据”，复杂的问题通过引入恰当的潜在数据，能够有效地解决我们的问题。

2、预备知识

介绍EM算法之前，我们需要介绍极大似然估计以及Jensen不等式。

2.1 极大似然估计

（1）举例说明：经典问题——学生身高问题

我们需要调查我们学校的男生和女生的身高分布。假设你在校园里随便找了100个男生和100个女生。他们共200个人。将他们按照性别划分为两组，然后先统计抽样得到的100个男生的身高。假设他们的身高是服从正态分布的。但是这个分布的均值μμ和方差σ2σ2我们不知道，这两个参数就是我们要估计的。记作θ=[μ,σ]Tθ=[μ,σ]T。

问题：我们知道样本所服从的概率分布的模型和一些样本，需要求解该模型的参数。如图1

图1

我们已知的有两个：样本服从的分布模型、随机抽取的样本；我们未知的有一个：模型的参数。根据已知条件，通过极大似然估计，求出未知参数。总的来说：极大似然估计就是用来估计模型参数的统计学方法。

（2）如何估计

问题数学化：设样本集X=x1,x2,…,xNX=x1,x2,…,xN,其中N=100N=100 ，p(xi|θ)p(xi|θ)为概率密度函数，表示抽到男生xixi（的身高）的概率。由于100个样本之间独立同分布，所以我同时抽到这100个男生的概率就是他们各自概率的乘积，也就是样本集XX中各个样本的联合概率，用下式表示：

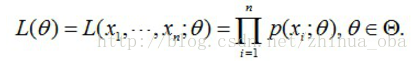
这个概率反映了，在概率密度函数的参数是θθ时，得到XX这组样本的概率。我们需要找到一个参数θθ，使得抽到XX这组样本的概率最大，也就是说需要其对应的似然函数L(θ)L(θ)最大。满足条件的θθ叫做θθ的最大似然估计量，记为

θ^= a r g m a x L (θ)

（3）求最大似然函数估计值的一般步骤

首先，写出似然函数：

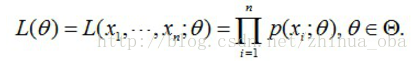
然后，对似然函数取对数：

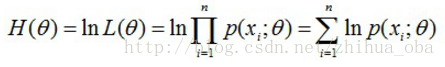
接着，对上式求导，令导数为0，得到似然方程；

最后，求解似然方程，得到的参数θθ即为所求。

2.2 Jensen不等式

设ff是定义域为实数的函数，如果对于所有的实数xx，f(x)f(x)的二次导数大于等于0，那么ff是凸函数。

Jensen不等式表述如下：如果ff是凸函数，XX是随机变量，那么：E[f(X)]≥f(E[X])E[f(X)]≥f(E[X])。当且仅当XX是常量时，上式取等号。其中，E[x]E[x]表示xx的数学期望。

例如，图2中，实线ff是凸函数，XX是随机变量，有0.5的概率是aa，有0.5的概率是bb。XX的期望值就是aa和bb的中值了，图中可以看到E[f(X)]≥f(E[X])E[f(X)]≥f(E[X])成立。

注： Jensen不等式应用于凹函数时，不等号方向反向。当且仅当XX是常量时，Jensen不等式等号成立。

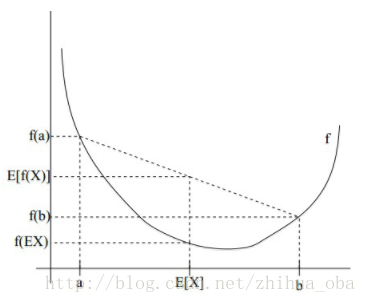图2

3、EM算法详解

3.1 问题描述

我们目前有100个男生和100个女生的身高，共200个数据，但是我们不知道这200个数据中哪个是男生的身高，哪个是女生的身高。假设男生、女生的身高分别服从正态分布，则每个样本是从哪个分布抽取的，我们目前是不知道的。这个时候，对于每一个样本，就有两个方面需要猜测或者估计：这个身高数据是来自于男生还是来自于女生？男生、女生身高的正态分布的参数分别是多少？EM算法要解决的问题正是这两个问题。如图3：

图3

3.2 EM算法推导

样本集X={

x1,…,xm}X={x1,…,xm}，包含mm个独立的样本；每个样本xixi对应的类别zizi是未知的（即上文中每个样本属于哪个分布是未知的）；我们需要估计概率模型p(x,z)p(x,z)的参数θθ，即需要找到适合的θθ和zz让L(θ)L(θ)最大。根据上文2.1 极大似然估计中的似然函数取对数所得logL(θ)logL(θ)，可以得到如下式：

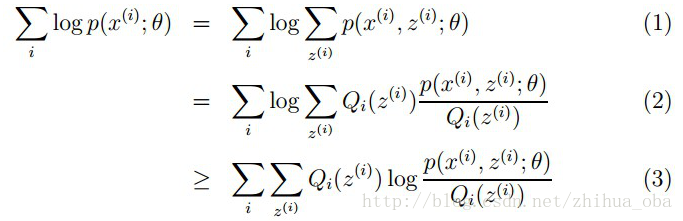
其中，(1)式是根据xixi的边缘概率计算得来，(2)式是由(1)式分子分母同乘一个数得到，(3)式是由(2)式根据Jensen不等式得到。

这里简单介绍一下(2)式到(3)式的转换过程：由于∑Qi(z(i))[p(x(i),z(i);θ)Qi(z(i))]∑Qi(z(i))[p(x(i),z(i);θ)Qi(z(i))]为p(x(i),z(i);θ)Qi(z(i))p(x(i),z(i);θ)Qi(z(i))的期望，且log(x)log(x)为凹函数，根据Jensen不等式（当ff是凸函数时，E[f(X)]≥f(E[X])E[f(X)]≥f(E[X])成立；当ff是凹函数时，E[f(X)]≤f(E[X])E[f(X)]≤f(E[X])成立）可由(2)式得到(3)式。此处若想更加详细了解，可以参考博客。

上述过程可以看作是对logL(θ)logL(θ)（即L(θ)L(θ)）求了下界。对于Qi(z(i))Qi(z(i))的选择，有多种可能，那么哪种更好呢？假设θθ已经给定，那么logL(θ)logL(θ)的值就取决于Qi(z(i))Qi(z(i))和p(x(i),z(i))]p(x(i),z(i))]了。我们可以通过调整这两个概率使下界不断上升，以逼近logL(θ)logL(θ)的真实值，那么什么时候算是调整好了呢？当不等式变成等式时，说明我们调整后的概率能够等价于logL(θ)logL(θ)了。按照这个思路，我们要找到等式成立的条件。根据Jensen不等式，要想让等式成立，需要让随机变量变成常数值，这里得到：

p ( x ( i ) , z ( i ) ; θ ) Q i ( z ( i ) ) = c

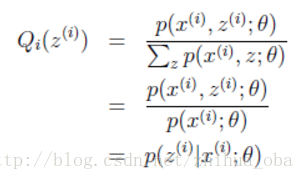
至此，我们推出了在固定其他参数θθ后，Qi(z(i))Qi(z(i))的计算公式就是后验概率，解决了Qi(z(i))Qi(z(i))如何选择的问题。这一步就是E步，建立logL(θ)logL(θ)的下界。接下来的M步，就是在给定Qi(z(i))Qi(z(i))后，调整θθ，去极大化logL(θ)logL(θ)的下界（在固定Qi(z(i))Qi(z(i))后，下界还可以调整的更大）。这里读者可以参考文章。

3.3 EM算法流程

初始化分布参数θθ；重复E、M步骤直到收敛：

E步骤：根据参数θθ初始值或上一次迭代所得参数值来计算出隐性变量的后验概率（即隐性变量的期望），作为隐性变量的现估计值：

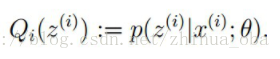
M步骤：将似然函数最大化以获得新的参数值：

你可能感兴趣的文章